Filters¶

The plastimatch filter command is a convenient method for performing common filters on images. This documentation is intended to explain in more detail the mathematics and implementation of these filters.

Gabor¶

The Gabor filter is a complex filter, and has real and imaginary components. Plastimatch implements only a uniform and symmetric form of the Gabor kernel, which is described as:

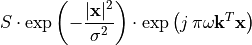
$S \cdot \mathrm{exp} \left( -\frac{|{\bf x}|^2}{\sigma^2} \right) \cdot \mathrm{exp} \left( j \, \pi \omega {\bf k}^T {\bf x} \right)$

Where x is the voxel position (relative to the center of the kernel), :sigma: is the filter width, and S is an arbitrary scaling factor. The vector k is the direction of modulation, and the frequency of modulation is given by :omega:. Note that the vector k is internally normalized to be a unit vector by plastimatch, so that larger k vectors do not increase the modulation.

The value of k can be set manually, or can be selected according to lie on a Fibanocci spiral. The Fibanocci spiral method is convenient for choosing a set of k vectors that are approximately evenly spaced on the unit sphere.

The values for :omega: and :sigma: can be interlinked. If :omega: is set, but :sigma: is not set, or vice versa, the other will be set automatically according to the following formula, which seems to work well:

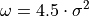
$\omega = 4.5 \cdot \sigma^2$

At the current time, only the real component of the Gabor filter is generated.

Gauss¶

The cannonical form for a Gaussian kernel is given as

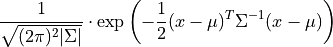
$\frac{1}{\sqrt{(2\pi)^2|\Sigma|}} \cdot \mathrm{exp} \left( -\frac{1}{2}(x-\mu)^T \Sigma^{-1} (x-\mu) \right)$

Note: because plastimatch uses a fixed width convolution kernel, the above expression may not sum to unity. Therefore, an empirical factor S is used instead.

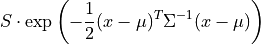
$S \cdot \mathrm{exp} \left( -\frac{1}{2}(x-\mu)^T \Sigma^{-1} (x-\mu) \right)$

Kernel¶

To be written.